Finite Impulse Response Filters Using Apple's Accelerate Framework - Part I
I’ve been working on an Audio DSP library for iOS/OSX and have been leveraging a lot of the operations in the Accelerate Framework. In this post I’ll go over some of the background theory behind FIR filters. Then I’ll walk through a basic implementation of a Finite Impulse Response (FIR) filter. In the next few posts, I will show you how to take advantage of some of the vectorized operations in the Accelerate Framework.
FIR Filters
Finite Impulse Response (FIR) filters are a class of digital filters which are based on a feed-forward difference equation. This is in contrast to Infinite Impulse Response (IIR) filters which have both feed-forward and feed-back terms. FIR Filters generally require a higher order to realize a given filter characteristic than an IIR filter, but have the advantages of guaranteed stability, and the ability to easily implement linear phase filters. FIR filters also have some characteristics that make them very well suited for multirate signal processing applications, which I will show in a later post.
The FIR filter difference equation for a discrete-time signal x, output y, and filter coefficients h at sample n is as follows:
$$y_{[n]} = h_{0}x_{[n]} + h_{1}x_{[n-1]} + h_{2}x_{[n-2]} + … + h_{M}x_{[n-M]}$$
This can be represented with the following block diagram. As you can see the architecture consists of a tapped delay line, with each tap corresponding to one of the filter coefficients.
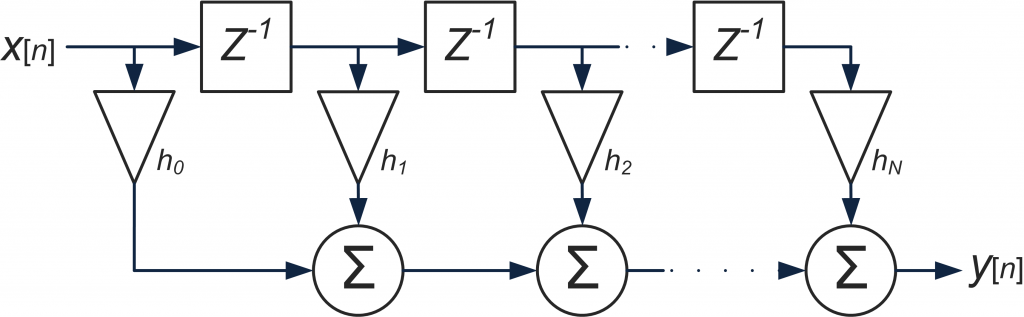
If we re-organize the previous equation as a weighted sum of the current sample and M previous samples, we get the following equation, which may look somewhat familiar:
$$y_{[n]} = \sum_{m=0}^{M}h_{[m]}x_{[n-m]}$$
That equation looks a lot like the equation for convolution, with the only difference being that the sum is over \([0, M]\) rather than over \([-\infty, \infty]\). If you think of h as extending to infinity in both directions, with all the samples outside \([0, M]\) set to zero, you can see that the only terms that contribute to the output are when m is within the range \([0,M]\). Therefore this difference equation is equivalent to the convolution of \(x\) and \(h\):
$$y_{[n]} = \sum_{m=-\infty}^{\infty}h_{[m]}x_{[n-m]} = (x \ast h)_{[n]}$$
Impmlementing Convolution
This can be implemented as two nested loops, over n and m respectively, and a little bit of bounds checking. A straightforward implementation is shown below:
/* Convolve x with h and store the result in output.
* output must be able to store at least x_length + h_length - 1 samples.
*/
void
convolve( const float *x,
unsigned x_length,
const float *h,
unsigned h_length,
float *output)
{
// The length of the result from linear convolution is one less than the
// sum of the lengths of the two inputs.
unsigned result_length = x_length + h_length - 1;
// Loop over the sample index m
for (unsigned n = 0; n < result_length; ++n)
{
// Clamp summation index so we don't try to index outside of x or h
unsigned m_min = (n >= (h_length - 1)) ? n - (h_length - 1) : 0;
unsigned m_max = (n < x_length - 1) ? n : x_length - 1;
// Initialize the output sample to 0
output[n] = 0;
for (unsigned m = m_min; m <= m_max; ++m)
{
// And accumulate the sum of the weighted filter taps
output[n] += h[m] * x[n - m];
}
}
}
With a working convolution function it looks like we are 99% done with our simple FIR filter, however there are still a few issues we have yet to address.
In most practical situations, we won’t be processing the entire signal at once. If we want to use this filter in any sort of real-time application, the filter will have to process blocks of data at a time. In almost every case, these blocks of data are going to be a continuous stream, so we need to make sure there are no boundary effects when we start processing a new block. To do this we need a way to store the state of the filter across calls to convolve. As you can see from the above implementation, the length of the output of convolve is x_length + h_length – 1. For an input of x_length samples, we expect an output of the same length, so it turns out that we can store the last h_length – 1 samples from the output (the overlap), and add them element-wise to the first h_length – 1 samples of the next block. This is commonly referred to as the overlap-and-add method. Here’s our updated FIR filter function:
Basic FIR Filter
/* filter signal x with filter h and store the result in output.
* output must be at least as long as x
*/
void
fir_filter( const float *x,
unsigned x_length,
const float *h,
unsigned h_length,
float *output)
{
// Create buffer to store overflow across calls
static float overflow[h_length - 1] = {0.0};
// The length of the result from linear convolution is one less than the
// sum of the lengths of the two inputs.
unsigned result_length = x_length + h_length - 1;
unsigned overlap_length = result_length - x_length;
// Create a temporary buffer to store the entire convolution result
float temp_buffer[result_length];
// Loop over the sample index m
for (unsigned n = 0; n < result_length; ++n)
{
// Clamp summation index so we don't try to index outside of x or h
unsigned m_min = (n >= (h_length - 1)) ? n - (h_length - 1) : 0;
unsigned m_max = (n < x_length - 1) ? n : x_length - 1;
// Initialize the output sample to 0
temp_buffer[n] = 0;
for (unsigned m = m_min; m <= m_max; ++m)
{
// And accumulate the sum of the weighted filter taps
temp_buffer[n] += h[m] * x[n - m];
}
}
// Now we need to add the overlap from the previous run,
// and store the overlap from this run for next time.
for (unsigned i = 0; i < overlap_length; ++i)
{
temp_buffer[i] += overflow[i];
overflow[i] = temp_buffer[x_length + i];
}
// write the final result to the output
for (unsigned j = 0; j < x_length; ++j)
{
output[j] = temp_buffer[j];
}
}
Now we have a working FIR filter that we can start using today! In Part II we will take a look at ways to speed this up using some of the operations in the Accelerate Framework.